Entonces, comencemos con las diferencias entre la matriz de una dimensión y la de dos dimensiones junto con un cuadro de comparación.
Gráfica comparativa:
| Bases para la comparación | Unidimensional | Bidimensional |
|---|---|---|
| BASIC | Almacenar lista única de elementos de tipo de datos similares. | Almacene 'lista de listas' o 'matriz de matrices' o 'matriz de matrices unidimensionales'. |
| Declaración | / * declaración en C ++ escriba variable_name [tamaño]; * / / * declaración en Java escriba variable_name []; nombre_variable = nuevo tipo [tamaño]; * / | / * declaración en C ++ escriba variable_name [size1] [size2]; * / / * declaración en Java escriba variable_name = new int [size1] [size2]; * / |
| Declaración alternativa | / * En Java int [] a = new int [10]; * / | / * En Java int [] [] a = new int [10] [20]; * / |
| Tamaño total en bytes | Bytes totales = sizeof (tipo de datos de la variable de matriz) * tamaño de la matriz. | Bytes totales = sizeof (tipo de datos de la variable de matriz) * tamaño del primer índice * tamaño del segundo índice. |
| Parámetro de recepción | Se puede recibir en un puntero, una matriz de tamaño o una matriz sin tamaño. | El parámetro que lo recibe debe definir la dimensión más a la derecha de una matriz. |
| Dimensiones | Unidimensional | Bidimensional |
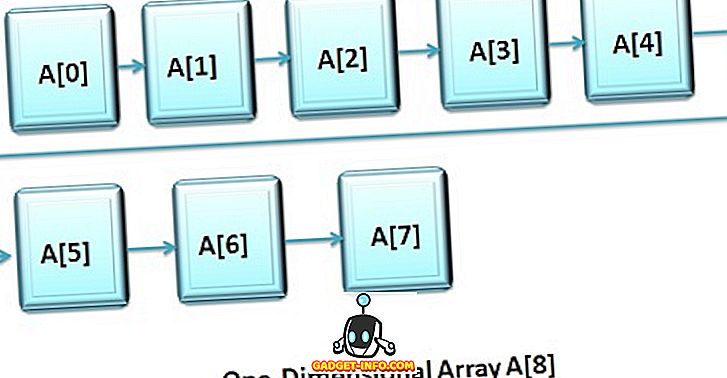
Definición de matriz unidimensional (matriz 1-D)
La matriz unidimensional o de una sola dimensión se considera como la "lista de variables de tipos de datos similares", y se puede acceder a cada variable especificando su índice entre corchetes precedido por el nombre de esa matriz.
Vamos a discutir en el contexto de C ++
// declaración en C ++ tipo variable_name [tamaño];
Aquí el tipo declara el tipo de datos de la variable de matriz y el tamaño define el número de elementos que la matriz contendrá.
Por ejemplo, si queremos declarar una matriz que contendrá el saldo de cada mes del año.
// ejemplo int month_balance [12];
Month _balance es la variable de matriz que contendrá los 12 enteros, que representarán el saldo de cada mes. Ahora, si queremos acceder al saldo del mes 'Abril', simplemente tuvimos que mencionar el nombre de la variable seguido del corchete que contiene el valor del índice para el mes de abril, es decir 'month_balance [3]'. Pero como 'abril' es el cuarto mes del año, pero habíamos mencionado '[3]' porque todas las matrices tienen 0 como el índice de su primer elemento.
En Java, esto se puede hacer como
// declaración en Java tipo variable_name []; nombre_variable = nuevo tipo [tamaño];
Aquí, inicialmente habíamos declarado una variable de matriz con su tipo y luego le habíamos asignado memoria usando 'nuevo' y la asignación 'nueva' a la variable de matriz declarada. Tomemos el ejemplo anterior si queremos declarar una matriz que contendrá el saldo en cada mes del año.
// ejemplo int month_balance []; month_balance = new int [12];
Aquí, 'nuevo' asigna memoria a la variable de la matriz "month_balance", por lo que ahora, mont_balance ahora tendrá la memoria para 12 valores enteros.
Las matrices se pueden inicializar cuando se declaran. Un inicializador de matriz es la lista de valores separados por comas rodeados por llaves.
//ejemplo
int month_balance = {100, 500, 200, 750, 850, 250, 630, 248, 790, 360, 450, 180}; Definición de matriz bidimensional (matriz bidimensional)
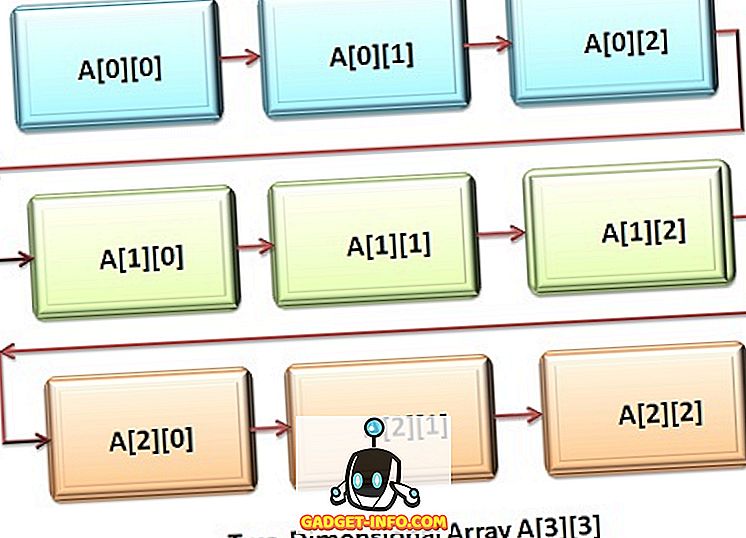
Tanto C ++ como Java admiten matrices multidimensionales. Una de las formas más simples de una matriz multidimensional es una matriz bidimensional o una matriz bidimensional. Una matriz bidimensional se puede considerar como "matriz de matrices" o "matriz de matrices unidimensionales". Para declarar la variable de matriz bidimensional, debemos especificar el nombre de la matriz seguido de dos corchetes, donde el segundo índice es el segundo conjunto de corchetes.
Una matriz bidimensional se almacena en la forma de la matriz fila-columna, donde el primer índice indica la fila y el segundo índice indica la columna. El segundo o el índice más a la derecha de una matriz cambia muy rápidamente en comparación con el primer índice o el más a la izquierda al acceder a los elementos de una matriz.
// declaración en C ++ tipo variable_name [size1] [size2];
Por ejemplo, queremos almacenar el saldo de cada 30 días en cada mes del año, en una matriz 2-D.
// ejemplo int month_balance [12] [30];
En Java, la matriz bidimensional se obtiene mediante
// declaración en Java tipo variable_name = new int [size1] [size2]; // ejemplo int month_balance = new int [12] [30];
Como no podemos pasar la matriz completa como un parámetro a una función, se pasa un puntero al primer elemento de la matriz. Un argumento que recibe la matriz bidimensional debe definir que es la dimensión más a la derecha. La dimensión más a la derecha es necesaria porque el compilador la necesita, para confirmar la longitud de cada fila si desea indexar la matriz correctamente. Si no se menciona el índice más a la derecha, el compilador no puede determinar dónde comienza la siguiente fila.
// ejemplo en Java void receiveing_funct (int a [] [10]) {. . . } Cuando la memoria se asigna dinámicamente a la matriz bidimensional en Java, se especifica el índice más a la izquierda, y las dimensiones restantes se pueden asignar por separado, es decir, todas las filas de la matriz pueden no ser del mismo tamaño.
// ejemplo en Java int month_balance = new int [12] []; month_balance [0] = new int [31]; month_balance [1] = new int [28]; month_balance [2] = new int [31]; month_balance [3] = new int [30]; month_balance [4] = new int [31]; month_balance [5] = new int [30]; month_balance [6] = new int [31]; month_balance [7] = new int [30]; month_balance [8] = new int [31]; month_balance [9] = new int [30]; month_balance [10] = new int [31]; month_balance [11] = new int [30]; month_balance [12] = new int [31];
Pero no hay ninguna ventaja de hacerlo.
Diferencias clave entre la matriz unidimensional y bidimensional
- La matriz unidimensional es una lista cuyos elementos son de tipo de datos similar. Por otro lado, la matriz bidimensional es una lista cuyos elementos son la matriz de un tipo de datos similar.
- En C ++, cuando la matriz unidimensional es recibida por el parámetro de una función de recepción, no es necesario mencionar el tamaño de la matriz, ya que el compilador entiende que la matriz del tipo (tipo de datos mencionado junto con el parámetro) con cierta longitud es para ser recibido. En una matriz bidimensional, el segundo índice, o el más a la derecha, debe especificarse, ya que el compilador debe saber dónde comienza una única fila y una nueva fila.
- En C ++, la matriz unidimensional se almacena en una ubicación de memoria contigua en el orden indexado, mientras que la matriz bidimensional también se almacena en la ubicación de memoria contigua, pero como hay múltiples filas en una matriz bidimensional, el almacenamiento de una primera fila es seguida por una segunda y la tercera y así sucesivamente.
Nota:
Pasar tanto la matriz unidimensional como la matriz bidimensional a una función es similar, es decir, ambas se pasan solo con el nombre de la matriz
// ejemplo passing_funt (name_of_array);
Conclusión:
Tanto en la matriz unidimensional como en la bidimensional, el índice juega un papel muy importante porque es lo único que identifica específicamente un elemento en la matriz. Tanto la matriz unidimensional como la bidimensional se pueden inicializar en el momento de su declaración.