Una medida ideal de tendencia central es aquella que está claramente definida, es fácil de entender, simplemente calculable. Debería estar basado en todas las observaciones y menos afectado por las observaciones extremas presentes en el conjunto de datos.
La gente suele contrastar estas dos medidas, pero el hecho es que son diferentes. Este artículo destaca específicamente las diferencias básicas entre la media y la mediana. Echar un vistazo.
Gráfica comparativa
| Bases para la comparación | Media | Mediana |
|---|---|---|
| Sentido | La media se refiere al promedio simple del conjunto dado de valores o cantidades. | La mediana se define como el número del medio en una lista ordenada de valores. |
| ¿Qué es? | Es un promedio aritmético. | Es media posicional. |
| Representa | Centro de gravedad del conjunto de datos. | Centro de gravedad del conjunto de datos. Punto medio del conjunto de datos |
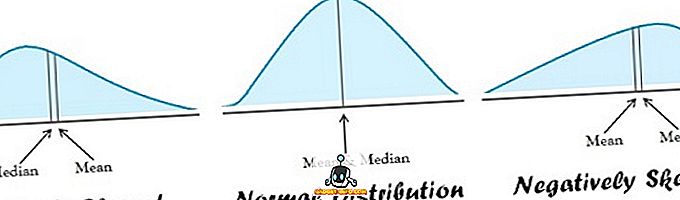
| Aplicabilidad | Distribución normal | Distribución sesgada |
| Outliers | La media es sensible a los valores atípicos. | La mediana no es sensible a los valores atípicos. |
| Cálculo | La media se calcula sumando todas las observaciones y luego dividiendo el valor obtenido con el número de observaciones. | Para calcular la mediana, el conjunto de datos se organiza en orden ascendente o descendente, luego el valor que cae en la mitad exacta del nuevo conjunto de datos, es la mediana. |
Definición de la media
La media es la medida ampliamente utilizada de la tendencia central, que se define como el promedio del conjunto de valores. Representa el modelo y el valor más común del rango de valores dado. Se puede calcular, tanto en series discretas como continuas.
La media es igual a la suma de todas las observaciones dividida por el número de observaciones en el conjunto de datos. Si el valor asumido por una variable es igual, su media también será igual. La media puede ser de dos tipos, la media muestral (x̅) y la media poblacional (µ). Se puede calcular con la fórmula dada:
- Media aritmética
n = número de valores - Para series discretas :
- Para servicios continuos :
A = media supuesta
C = divisor común
Definición de la mediana
La mediana es otra medida importante de la tendencia central, utilizada para dividir el valor en dos partes iguales, es decir, la mitad mayor de la muestra, la población o la distribución de probabilidad de la mitad inferior. Es el valor más intermedio, que se logra cuando las observaciones se clasifican en un orden específico, ya sea ascendente o descendente.
Para el cálculo de la mediana, en primer lugar, organice las observaciones de menor a mayor o de mayor a menor, luego aplique la fórmula apropiada, según las condiciones que se indican a continuación:
- Si el número de observaciones es impar :
- Si el número de observaciones es par :
- Para series continuas :
c = frecuencia acumulada de la clase media precedente
f = frecuencia de la clase media
h = ancho de la clase
Diferencias clave entre la media y la mediana
Las diferencias significativas entre la media y la mediana se proporcionan en el siguiente artículo:
- En las estadísticas, una media se define como el promedio simple del conjunto dado de valores o cantidades. Se dice que la mediana es el número medio en una lista ordenada de valores.
- Mientras que la media es el promedio aritmético, la mediana es el promedio posicional, en esencia, la posición del conjunto de datos determina el valor de la mediana.
- La media describe el centro de gravedad del conjunto de datos, mientras que la mediana resalta el valor más central del conjunto de datos.
- La media es apropiada para datos normalmente distribuidos. En el otro extremo, la mediana es la mejor cuando la distribución de datos está sesgada.
- La media está muy afectada por el valor extremo que no está en el caso de una mediana.
- La media se calcula sumando todas las observaciones y luego dividiendo el valor obtenido con el número de observaciones; el resultado es malo A diferencia de la mediana, el conjunto de datos se organiza en orden ascendente o descendente, entonces el valor que cae en la mitad exacta del nuevo conjunto de datos es la mediana.
Ejemplo
Encuentra la media y la mediana del conjunto de datos dado:
58, 26, 65, 34, 78, 44, 96
Solución: para calcular la media, debe dividir la suma de las observaciones con el número de observaciones,
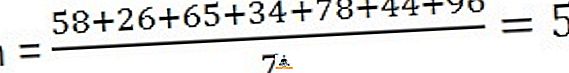
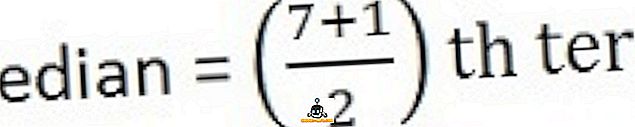
Para calcular la mediana, en primer lugar, ordene la serie en una secuencia, es decir, de menor a mayor,
26, 34, 44, 58, 65, 78, 96
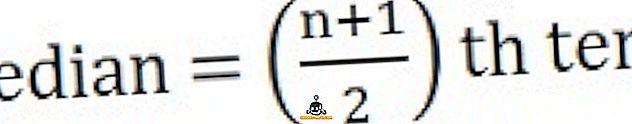
Conclusión
Después de revisar los puntos anteriores, podemos decir que estos dos conceptos matemáticos son diferentes. La media aritmética o media se considera la mejor medida de la tendencia central, ya que contiene todas las características de una medida ideal, pero tiene el inconveniente de que las fluctuaciones de muestreo influyen en la media.
De la misma manera, la mediana también se define sin ambigüedad y es fácil de entender y calcular, y lo mejor de esta medida es que no se ve afectada por las fluctuaciones de muestreo, pero la única desventaja de la mediana es que no se basa en todas observaciones Para la clasificación de final abierto, la mediana normalmente se prefiere a la media.
